PENALARAN UMUM - PENALARAN LOGIS
DAFTAR ISI
- Pengertian Pernyataan
- Pengertian Ingkaran atau Negasi
- Pernyataan Majemuk
- Disjungsi
- Konjungsi
- Implikasi
- Biimplikasi
- Kuantor Universal dan Kuantor Eksistensial
- Kuantor Universal
- Kuantor Eksistensial
- Penarikan Kesimpulan
- Silogisme
- Modus Ponens
- Modus Tolens
A. Pengertian Pernyataan
pengertian pernyataan. Pernyataan disebut juga kalimat deklaratif, yaitu kalimat yang hanya bernilai benar atau salah. Artinya, pernyataan tidak bisa bernilai benar dan salah sekaligus. Benar tidaknya suatu pernyataan bisa kamu sesuaikan dengan keadaan aslinya. Contohnya sebagai berikut. Telepon genggam merupakan salah satu alat komunikasi. (Pernyataan benar) Semua ikan bernapas menggunakan paru-paru. (Pernyataan salah)
B. Pengertian Ingkaran atau Negasi
Ingkaran atau negasi adalah pernyataan baru yang merupakan lawan dari pernyataan semula. Jika pernyataan semula bernilai benar, maka pernyataan barunya bernilai salah. Sebaliknya, jika pernyataan semula bernilai salah, maka pernyataan barunya bernilai benar. Perhatikan permisalan berikut.
Jika pernyataan (p) bernilai benar (B), maka ingkarannya (~p) bernilai salah (S).
Jika pernyataan (p) bernilai salah (S), maka ingkarannya (~p) bernilai benar (B).
Untuk lebih jelasnya, simak contoh berikut.
Contoh 1 :
p = Hari ini turun hujan
~p = Hari ini tidak turun hujan
Contoh 2 :
p = Ibu pergi menggunakan mobil
~q = Ibu pergi tidak menggunakan mobil
C. Pernyataan Majemuk
Pernyataan majemuk adalah pernyataan yang terdiri dari dua atau lebih pernyataan tunggal yang terhubung oleh kata penghubung logika, seperti "dan" (conjunction), "atau" (disjunction), "jika... maka" (implication),atau "jika dan hanya jika" (biconditional). Pernyataan majemuk dapat menggabungkan pernyataan tunggal untuk membentuk pernyataan yang lebih kompleks dan memungkinkan analisis logika yang lebih rinci.
1. Disjungsi
Disjungsi adalah pernyataan majemuk yang dihubungkan oleh kata hubung ‘atau’.
Secara matematis, disjungsi ditulis sebagai p v q yang berarti ‘p atau q’.
Perhatikan contoh berikut.
p = sekolah libur pada hari sabtu
q = sekolah libur pada hari minggu
(p v q) disjungsi = sekolah libur pada hari sabtu atau minggu
Suatu disjungsi akan bernilai benar jika salah satu pernyataan bernilai benar atau kedua pernyataan (p dan q) bernilai benar.
1.1 Ingkaran Disjungsi
~(p v q) ≡ ~p ˄ ~q
Perhatikan contoh berikut.
p v q = sekolah libur pada hari sabtu atau minggu
~(p v q) ≡ ~p ˄ ~q
~p ˄ ~q ingkaran disjungsi = sekolah tidak libur pada hari sabtu dan minggu
tabel kebenaran disjungsi :
_________________
| p | q | p v q |
| B | B | B |
| S | S | S |
| B | S | B |
| S | B | B |
-----------------
2. Konjungsi
Konjungsi adalah kalimat majemuk yang dihubungkan oleh tanda hubung ‘dan’.
Secara matematis, dilambangkan sebagai p ˄ q. Untuk lebih jelasnya, simak contoh berikut.
p = Novi memiliki hewan peliharaan kucing
q = Novi memiliki hewan peliharaan kelinci
(p ^ q) Konjungsi = Novi memiliki hewan peliharaan kucing dan kelinci
Konjungsi akan bernilai benar jika dua pernyataan (p dan q) bernilai benar (B).
Jika salah satu pernyataan salah, nilai kebenaran konjungsi juga akan salah (S).
2.1 Ingkaran Konjungsi
Untuk ingkaran konjungsi, memenuhi persamaan :
~(p ˄ q) ≡ ~p v ~q
Berikut contohnya.
(p ^ q) Konjungsi = Novi memiliki hewan peliharaan kucing dan kelinci
~(p ˄ q) ≡ ~p v ~q
~p v ~q ingkaran konjungsi = Novi tidak memiliki hewan poeliharaan kucing atau kelinci
tabel kebenaran konjungsi :
_________________
| p | q | p ^ q |
| B | B | B |
| S | S | S |
| B | S | S |
| S | B | B |
-----------------
3. Implikasi
Implikasi adalah pernyataan majemuk sebab akibat yang dihubungkan oleh ‘jika…, maka…’ atau
jika p, maka q. secara matematis, dilambangkan p => q.
Dalam hal ini, p disebut sebagai anteseden (penyebab), sedangkan q disebut konsekuen (akibat). Implikasi akan bernilai benar jika:
- p bernilai benar dan q bernilai benar, maka implikasinya benar;
- p bernilai salah dan q bernilai benar, maka implikasinya benar;
- p bernilai salah dan q bernilai salah, maka implikasinya benar; dan
- p bernilai benar dan q bernilai salah, maka implikasinya bernilai salah.
Adapun jenis-jenis implikasi adalah sebagai berikut.
- Konvers dari implikasi p => q adalah q => p.
- Invers dari implikasi p => q adalah ~p => ~q.
- Kontraposisi dari implikasi p => q adalah ~q => ~p.
3.1 Ingkaran/Negasi Implikasi
negasi p => q adalah p ^ ~q atau ditulis
~(p => q) ≡ p ˄ ~q
Untuk lebih jelasnya, simak contoh berikut.
p = Betty mendapatkan uang di hari jum'at
q = Betty pergi ke yogyakarta
p => q = Jika Betty mendapatkan uang di hari jum'at maka betty pergi ke yogyakarta
~(p => q) ≡ p ˄ ~q ingkaran implikasi = Betty mendapatkan uang di hari jum'at dan Betty tidak pergi ke yogyakarta
Tabel kebenaran implikasi :
__________________
| p | q | p => q |
| B | B | B |
| S | S | B |
| B | S | S |
| S | B | B |
------------------
4. Biimplikasi
Biimplikasi merupakan pernyataan majemuk (kalimat terbuka) yang dihubungkan dengan kata hubung ‘jika dan hanya jika …’.
Secara matematis dilambangkan sebagai p ⬄ q. Untuk lebih jelasnya, simak contoh soal berikut.
p = Lisa memberikan uang kepada adiknya
q = Lisa lulus ujian
p <=> q = Lisa akan memberikan uang kepada adiknya jika dan hanya jika ia lulus ujian
Tabel Kebenaran biimplikasi :
___________________
| p | q | p <=> q |
| B | B | B |
| S | S | B |
| B | S | S |
| S | B | S |
-------------------
D. Kuantor Universal dan Kuantor Eksistensial
1. Kuantor Universal
Kuantor universal biasa disebut kuantor umum adalah bentuk ungkapan yang menyatakan
keseluruhan dan biasanya ditulis dengan kata ‘semua’ atau ‘setiap’.
Kedua kata merupakan kuantor universal karena menunjukkan bahwa semua anggota memiliki
keadaan yang sama. Secara matematis, dilambangkan sebagai ‘∀’.
Perhatikan contoh berikut.
“Semua gajah memiliki belalai”
Pada kalimat di atas, ‘memiliki belalai’ berperan sebagai predikat.
Jika predikatnya kamu simbolkan sebagai B, maka penulisannya menjadi G(x) ⇒ B(x).
Artinya, jika x adalah gajah maka x mempunyai belalai.
Eitss, kamu harus paham bahwa kalimat tersebut bukan kalimat kuantor universal karena belum
memuat kata ‘semua’. Agar menjadi kalimat kuantor universal,
kamu perlu menambahkan lambang kuantornya (∀), sehingga menjadi
(∀x)(G(x)) ⇒ B(x)
Setelah kamu tambah tanda kuantor universal, kalimatnya menjadi
“untuk semua x, jika x adalah gajah maka x memiliki belalai.”
2. Kuantor Eksistensial
Jika kuantor universal ditandai dengan kata ‘semua’, maka kuantor eksistensial ditandai dengan kata ‘beberapa’ atau ‘ada’.
Itulah mengapa kuantor eksistensial menunjukkan sesuatu yang bersifat khusus atau beberapa anggota yang memiliki
keadaan berbeda dengan lainnya. Secara matematis, disimbolkan sebagai ‘∃’.
Untuk lebih jelasnya, simak contoh berikut :
“Beberapa orang rajin beribadah”
Penulisan logika predikat untuk pernyataan di atas adalah
“ada x yang adalah orang dan x rajin beribadah”
(∃x)(Orang(x)) ∧ rajin beribadah atau menjadi (∃x)(O(x)) ∧ I(x)
E. Penarikan Kesimpulan
Kamu bisa melakukan penarikan kesimpulan dengan tiga metode, yaitu :
- silogisme
- modus ponens
- modus tolens
1. Silogisme
Silogisme merupakan penarikan kesimpulan dari dua pernyataan implikasi. Aturan silogisme adalah sebagai berikut.
Jika p => q benar dan q => r benar maka p => r benar, atau nyatakan dalam bentuk premis.
Premis 1: p => q
Premis 2: q => r
Kesimpulan: p => r
Contoh :
Premis 1 : Jika rumah tidak dikunci maka ibu pulang (p => q)
Premis 2 : Jika ibu pulang maka ayah pulang (q => r)
Kesimpulan : Jika rumah tidak dikunci maka ayah pulang (p => r)
2. Modus ponens
Modus ponens mengikuti aturan berikut ini.
Premis 1: p => q
Premis 2: p
Kesimpulan: q
Contoh :
Premis 1 :Jika Reni mengikut lomba tari maka reni rajin berlatih ( p => q )
Premis 2 : Reni mengikuti lomba tari (p)
Kesimpulan : Reni rajin berlatih (q)
3. Modus Tolens
Penarikan kesimpulan dengan modus tolens, mengikuti aturan berikut.
Jika p => q benar dan ~q benar maka ~p benar, bisa ditulis:
Premis 1: p => q
Premis 2: ~q
Kesimpulan: ~p
Premis 1 :Jika Reni mengikut lomba tari maka reni rajin berlatih ( p => q )
Premis 2 : Reni tidak rajin berlatih (~q)
Kesimpulan : Reni tidak mengikuti lomba tari (~p)
Contoh Soal (Bonus 1) :
Jika bahan kaus yang digunakan adalah katun maka penjualan kaus meningkat.
Jika penjualan kaus meningkat maka penjualan kemeja akan meningkat.
Penjualan kemeja mengalami penurunan.
Simpulan yang tepat adalah…
a. Penjualan kaus menurun.
b. Penjualan kemeja meningkat.
c. Bahan kaus yang digunakan bukan katun
d. Bahan kemeja yang digunakan adalah katun.
e. Pembeli tidak membeli kaus maupun kemeja
Premis 1 : p => q
Premis 2 : q => r
Premis 3 : ~r
Jawab :
Premis 1 : p => q(x)
Premis 2 : q(x) => r
====================
p = > r(x)
Premis 3 : ~r (x)
===================
~p
~p = Bahan kaus yang digunakan bukan katun
Jawaban benar adalah (C)
Contoh Soal (Bonus 2) :
Negasi dari invers pernyataan “Jika limbah
dibuang ke sungai maka populasi ikan
terancam” adalah …
A. Limbah dibuang ke sungai dan populasi ikan
tidak terancam
B. Populasi ikan terancam dan limbah tidak
dibuang ke sungai
C. Poluasi ikan tidak terancam atau limbah
dibuang ke sungai
D. Limbah tidak dibuang ke sungai dan populasi
ikan terancam
E. Limbah dibuang ke sungai atau populasi ikan
tidak terancam
p = jika limbah dibuang kesungai
q = populasi ikan terancam
~p = jika limbah tidak dibuang kesungai
~q = populasi ikan tidak terancam
Aturan
premis 1 : p => q
~p => ~q (inverse)
p => q
p ^ ~q (negasi)
~p ^ ~(~q)
========= (BELUM YAKIN)
~p v q
p => q
p ^ ~q (negasi)
============ (MASIH PERKIRAAN)
~p v q (abis dinegasikan terus di inverse)
negasi inversenya : ~p v q (mirip ada di aturan 6)
Jawaban benar adalah (D)
limbah tidak dibuang kesungai atau populasi ikan terancam
Bonus Cheatsheet Penarikan Kesimpulan :
Aturan 1
-----------
Premis 1 : p => q
premis 2 : p
=========
kesimpulan: q
Aturan 2
-----------
Premis 1 : p => q
premis 2 : ~q
=========
kesimpulan: ~p
Aturan 3
-----------
Premis 1 : p => q
premis 2 : ~p
=========
kesimpulan: ~p
Aturan 4
-----------
Premis 1 : p => q
premis 2 : q
=========
kesimpulan: tidak dapat disimpulkan
Aturan 5
-----------
Premis 1 : p => q
premis 2 : q => r
=========
kesimpulan: p => r
Aturan 6
-----------
Premis 1 : p => q
premis 2 : ~q => ~p
=========
kesimpulan: ~p v q
Rangkuman (Logika Matematika - Membuat Tabel Kebenaran) :
- Konjungsi (^) : pernyataan majemuk dengan kata hubung "dan"
Bernilai benar hanya jika kedua pernyataan benar
- Disjungsi (v) : pernyataan majemuk dengan kata hubung "atau"
Bernilai salah hanya jika kedua pernyataan salah
- Implikasi (⇒) : pernyataan majemuk dengan kata hubung "jika... maka..."
Bernilai salah jika anteseden benar dan konsequen salah
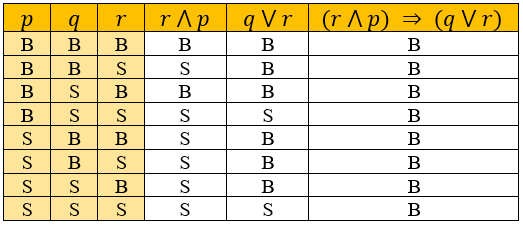
Misal p ⇒ q, bernilai salah ketika p benar dan q salahcontoh membuat Tabel kebenaran dari (r ∧ p) ⇒ (q∨r)
adalah:
Refferensi :
- Quipper (https://www.quipper.com/id/blog/masuk-ptn/sbmptn/informasi-sbmptn/penalaran-umum-penalaran-logis/#Pengertian_Ingkaran_atau_Negasi)
- Mbah Google :)